Distribusi Frekuensi

Distribusi Frekuensi Empiris

Distribusi Frekuensi Empiris adalah suatu daftar yang menunjukkan penggolongan kumpulan data diamana termasuk penentuan berapa bilangan yang termasuk ke dalam setiap golongan tersebut.

Tujuan dari penentuan Distribusi Frekuensi adalah untuk menyajikan data dalam bentuk yang lebih teratur dan ringkas sehingga lebih mudah untuk dipahami.

BAGIAN-BAGIAN DARI DITRIBUSI FREKUENSI

1. Variabel Penyelidikan
   Variabel Penyelidikan adalah obyek yang diselidiki
2. Nilai Variabel
   Nilai variable adalah nilai masing-masing penyelidikan / pengujian. Contoh :

Apabila seorang ahli beton mengadakan pengujian tentang kekuatan karakteristik beton dimana untuk mendapatkan kekuatan karakteristik diperlukan nilai masing-masing pengujian beton

Dari contoh diatas yang merupakan :

Variabel penyelidikan adalah pengujian kekuatan karakteristik beton dan Nilai variabel adalah nilai masing-masing pengujian beton Pada Umumnya Pembuatan Distrbusi Dapat Dibagi 3 Tahap :

1. Menentukan jumlah kelas , guna memasukkan angka-angka.
2. Memasukkan angka-angka ke kelas-kelas yang sesuai serta menghitung frekuensinya.
3. Membuat tabel distribusi frekuensi

Distribusi frekuensi dibagi 2 :

a. Distribusi Frekuensi Tunggal

b. Distribusi Frekuensi Bergolong

DISTRBUSI FREKUENSI TUNGGAL (DFT)

Distribusi Frekuensi Tunggal (DFT) adalah suatu pencaran frekuensi yang menunjukkan tidak adanya pengelompokkan nilai variabel.

Contoh :

Variabel Penyelidikan :

Penyelidikan tentang nilai mata kuliah Statistik Semester I

Mahasiswa Jurusan Teknik Sipil Politeknik UI tahun akademik 1993/1994 .

Nilai Variabel :
7             6	6	5	7	6	5	4	6	6
6             5	6	6	6	7	7	5	7	7
7             8	5	6	5	7	6	7	8	5
Dari angka-angak	tersebut	diatas kita	tidak	dapat	memperoleh gambaran

apa-apa. Untuk mendapatkan gambaran dan kesimpulan , kita perlu mengatur angka-angka itu menjadi suatu tabel.

Penyajian dalam bentukDistribusi Frekuensi Tunggal

Nilai Mata Kuliah Statistik Semester I Mahasiswa Jurusan Teknik Sipil

Politeknik UI tahun akademik 1993/1994 .

No.( i)	Nilai (Xi)	Frekuensi (f i)
1	4	1
2	5	7
3	6	11
4	7	9
5	8	2
k=5 Z=1	30

k = banyaknya kelas fi = frekuensi kelas ke i

= jumlah indek = 1 s/d k termasuk frekuensi ke 1 dan ke k

Dari tabel tersebut diatas kita dapat mengambil kesimpulan bahwa urutan data yang mempunyai frekuensi dari tertinggi ke terendah adalah : 6, 7, 5, 8, 4

Jumlah kolom yang ada pada panel yang ada pada tabel bukan merupakan syarat mutlak, jumlah kolom dalam tabel tergantung pada kebutuhan .

DISTRIBUSI FREKUENSI BERGOLONG (DFB)

Distribusi Frekuensi Bergolong (DFB) adalah suatu pencaran frekuensi yang menunjukkan adanya pengelompokkan nilai variabel dalam satu kelas.

No. (i)	Batas Kelas ( Xi)	Tanda Kelas (Mi)	Frekuen si (Fi)
Semu	Nyata
1	3-5	2,5 – 5,5	3	4
2	6-8	5,5 – 8,5	5	7
3	9-11	8,5-11,5	11	10
4	12 -14	11,5-14,5	13	13
A =”S Z=1	34

Istilah-istilah Yang Digunakan dalam Distribusi Frekuensi Bergolong :

1.     Kelas

Kelas adalah tiap-tiap kelompok nilai variabel.

Contoh :

Dalam tabel diatas terdapat 4 kelas dengan masing-masing kelas yaitu kelas pertama 3-5, kelas kedua 6-8, kelas ketiga 9-11 dan kelas keempat 12-14.

2.     Batas Kelas

Batas Kelas adalah nilai-nilai yang membatasi antara kelas yang satu dengan kelas yang lain .

Contoh :

Nilai 3 dan 5,6 dan 8,9 dan 11,12 dan 14.

3.     Batas Kelas Atas dan Batas Kelas Bawah

Batas Kelas Atas (Upper Limits) adalah nilai tertinggi dalam suatu kelas . Contoh :

Angka-angka pada deret sebelah kanan batas kelas yaitu 5,8,11 dan 14. Batas Kelas Bawah (Lower Limits) adalah nilai terndah dalam suatu kelas Contoh :

Angka-angka pada deret sebelah kanan batas kelas yaitu 3, 6, 9 dan 12

4.     Batas Kelas Semu dan Batas Kelas Nyata

Batas Kelas Semu adalah nilai yang terpisah antara batas kelas yang satu dengan batas kelas yang lain.

Contoh :

Nilai 5 dengan 6, 8 dengan 9, 11 dengan 12.

Batas Kelas Nyata adalah nilai yang sama antara batas kelas yang satu dengan batas kelas yang lain.

Contoh :

Nilai 2,5; 5,5; 8,5; 11,5; 14,5.

Nilai Batas Kelas Nyata = ^{BkasI + Bk}^^sB

2

Keterangan :

B k a s I : Batas kelas atas semu prioritas I

B k b s II : Batas kelas bawah semu prioritas II

5.     Lebar Kelas / Interval Kelas (I)

Lebar Kelas / Interval Kelas adalah jumlah nila-nilai variabel dalam tiap kelas.

Contoh :

Kelas 3-5 terdiri dari nilai – nilai variabel 3, 4, dan 5. Jadi tiap – tiap kelas terdiri dari 3 nilai variabel, sehingga interval kelas = 3

Interval Kelas (I) = Bkan-Bkbn dalam satu kelas

atau          =Bkasll-Bkasl

atau          =Bkbsll-Bkbsl

Keterangan :

B k a n     : Batas kelas atas nyata

B k b n     : Batas kelas bawah nyata

B k a s II : Batas kelas atas semu prioritas II

B k a s I : Batas kelas atas semu prioritas I

B k b s II : Batas kelas bawah semu prioritas II

B k b s I : Batas kelas bawah semu prioritas II

6.     Titik Tengah / Tanda Kelas / Class Mark (m i)

Titik Tengah / Tanda Kelas / Class Mark adalah nilai variabel yang terdapat di tengah-tengah antara Batas Kelas Atas dengan Batas Kelas

Bawah atau nilai yang mewakili tiap-tiap kelas .

Contoh :

Pada tabel diatas niali 4, 7, 10 dan13 merupakan tanda kelas.

         .         .        .     .. Bkb s/n-Bks s/n dalam satu kelas

Tanda Kelas (m i) =——————————————

Keterangan :

Bkb s/n : Batas kelas bawah semu / nyata

Bka s/n : Batas kelas atas semu / nyata

7.     Jarak Pengukuran / Range ( R )

Jarak Pengukuran / Range adalah nilai variabel tertinggi dikurangi dengan nilai variabel terendah dalam suatu pengujian . (Tidak perlu memandang batas nyatanya).

Hal-hal Yang Perlu Diperhatikan Dalam Pembuatan Diustribusi Frekuensi Bergolong (DFB):

1. Menentukan jumlah kelas, guna memasukkan angka-angka atau nilai-nilai variabel . Biasanya digunakan Aturan Sturges oleh H . A Sturges tahun

1926.

k= 1+3,3 log n ————— ► pembulatan ( 0,0 -0,9)

Keterangan :

k: Banyaknya kelas

n : Banyaknya data / pengamatan

• Menentukan interval kelas , guna memasukkan angka-angka atau nila- nilai variabel yang sesuai serta kemudian menghitung frekuensinya.

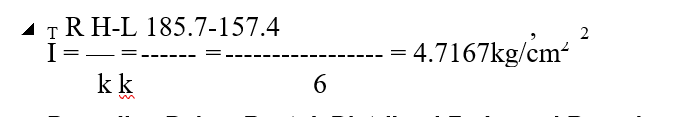
Keterangan :

I : Interval Kelas

R : Range

H : Nilai Variabel Tertinggi

L : Nilai Variabel Terndah

k: Banyaknya kelas

Contoh :

Hasil pemeriksaan keteguhan tekan beton (benda uji kubus dengan sisi 15 cm) sesudah 28 hari dengan campuran 1 : 1¹/2 : 2V2, yang dilaksanakan di Laboratorium Pengujian Bahan Politekni UI Depok dalam satuan kg/cm² .

157,4	167,8	171,2	174,7	177,4
157,7	168,4	172,4	175,1	178,8
162,2	168,7	173,2	175,5	179,2
164,2	169,9	173,6	176,0	181,3
165,8	170,2	174,7	176,1	185,7

data disusun secara acak satu angka dibelakang koma.

n        =25

H       = 185,7 kg/cm²

L        = 157,4       kg/cm²

Banyaknya Kelas (k)

k        =1+3,3       log n

= 1+3,3 log 25

= 5,6132

« 6

Interval Kelas (I)

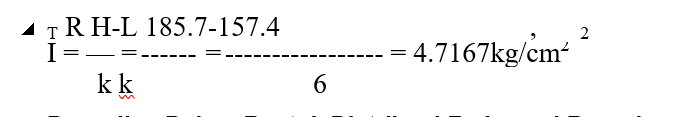
Penyajian Dalam Bentuk Distribusi Frekuensi Bergolong :

Hasil pemeriksaan keteguhan tekan beton (benda uji kubus dengan sisi 15 cm) sesudah 28 hari dengan campuran 1 : 2 : 3, yang dilaksanakan di

Laboratorium Pengujian Bahan Politekni UI Depok dalam satuan kg/cm² .

Kelas (i)	Batas Kelas Semu	(Xi) (Kg/Cm2) Nyata	Tanda Kelas (mi) (Kg/Cm2)	Frekuensi (fi)
1	157.4- 162.1	157.35-162.15	159.75	2
2	162.2 -0166.9	162.15-166.95	164.55	3
3	167.0-171.7	166.95-171.75	169.35	6
4	171.8-176.5	171.75-176.65	174.15	9
5	176.6-181.3	176.55-181.35	178.95	4
6	181.4-186.1	181.35-186.15	183.75	1
<5 Z=1	25

DISTRIBUSI FREKUENSI RELATIF (DFR)

Distribusi Frekuensi Relatif adalah pencaran frekuensi yang diperoleh dengan membagi frekuensi tiap-tiap kelas dengan banyaknya data pengamatan .]

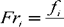
Keterangan :

Fri                 = Frekuensi Relatif Kelas ke i

fi                   = Frekuensi Kelas ke i

n                   = Banyaknya Data Pengamatan

Frekuensi Relatif bisa juga dibuat dengan bentuk persentase atau disebut juga Persentase Distribusi yang dapat diperoleh dengan mengalikan frekuensi relatif dengan 100%.

Fr₁(%)= — x 100%

n

Contoh :

Hasil pemeriksaan keteguhan tekan beton (benda uji kubus dengan sisi 15 cm) sesudah 28 hari dengan campuran 1:2:3, yang dilaksanakan di Laboratorium Pengujian Bahan Politekni UI Depok dalam satuan kg/cm² .

Kelas (i)	Tanda Kelas (mi) (Kg/Cm2)	Frekuensi (fi)	Fri	Fri (%)
1	159.75	2	0.08	8
2	164.55	3	0.12	12
3	169.35	6	0.24	24
4	174.15	9	0.36	36
5	178.95	4	0.16	16
6	183.75	1	0.04	4
	i> = 25 Z=1	ll	6 y Fri = 100% /=i

DISTRIBUSI FREKUENSI KOMULATIF (DFK)

Distribusi Frekuensi komulaitf adalah pencaran frekuensi yang merupakan penjumlahan-penjumlahan frekuensi-frekuensi kelas secara berurutan.

Sebagai akibat dari penjumlahan-penjumlahan antara frekuensi yang beurutan harus diperhatikan bahwa bentuk kelasnya sudah berubah sesuai dengan Distribusi Frekuensi Komulatif.

Distribusi Frekuensi Komulatif dibagi 2 :

1. Distribusi Frekuensi Komulatif (DFK) kurang dari
2. Distribusi Frekuensi Komulatif (DFK) lebih dari

Contoh :

a. DFK “kurang dari (<)” hasil pemeriksaan keteguhan tekan beton (benda uji kubus sisi 15 cm) sesudah 28 hari dengan campuran 1:2:3 yang
dilaksanakan di Laboratorium Pengujian Bahan Politeknik UI Depok dalam satuan kg/cm²

Batas Kelas Komulatif “<” (Xkj) (Kg/Cm2)	Frekuensi Komulatif “<” (Fki)
Kurang dari 157.35	0
Kurang dari 162.15	2
Kurang dari 166.95	5
Kurang dari 171.75	11
Kurang dari 176.55	20
Kurang dari 181.35	24
Kurang dari 186.15	25

b. DFK “lebih dari (>)” hasil pemeriksaan keteguhan tekan beton (benda uji kubus sisi 15 cm) sesudah 28 hari dengan campuran 1:2:3 yang dilaksanakan di Laboratorium Pengujian Bahan Politeknik UI Depok dalam satuan kg/cm².

Batas Kelas Komulatif “>” (Xkj) (Kg/Cm2)	Frekuensi Komulatif “<” (FK)
Lebih dari 157.35	25
Lebih dari 162.15	23
Lebih dari 166.95	20
Lebih dari 171.75	14
Lebih dari 176.55	5
Lebih dari 181.35	1
Lebih dari 186.15	0

PENYAJIAN DISTRIBUSI FREKUENSI DALAM BENTUK GRAFIK, DAN DIAGRAM

Dalam laporan-laporan tertulis, brosur, majalah, buku-buku, dan lain- lain sering kita lihat Distribusi Frekuensi disajikan dalam bentuk grafik dan diagram. Atau disajikan bersama-sama table Distribusi Frekuensi.

Guna penyajian Distribusi Frekuensi dalam bentuk grafik dan diagram adalah :

1. Mempertegas dan memperjelas Distribusi Frekuensi yang telah disajikan sebagai table/daftar.
2. Sebagai pengganti bagi Distribusi Frekuensi yang berbentuk sebagai daftar / tabel.

Grafik dan diagram yang sering dipakai untuk melukiskan distribusi frekuensi adalah :

1. Histogram frekuensi
2. Poligon frekuensi
3. Ogive frekuensi
4. Diagram lingkaran

HISTOGRAM FREKUENSI

Histogram frekuensi adalah suatu bentuk diagram yang terdiri dari persegi panjang dimana setiap persegi panjang tersebut mewakili/ menerangkan/ menggambarkan sebuah kelas dari distribusi frekuensi.

Contoh :

Histogram frekuensi hasil pemeriksaan keteguhan tekan beton (benda uji kubus sisi 15 cm) sesudah 28 hari dengan campuran 1:2:3 yang dilaksanakan dilaboratorium pengujian bahan Politeknik UI Depok dalam satuan kg/cm²

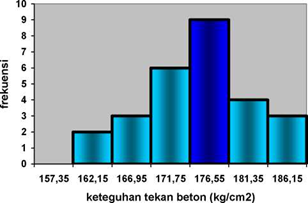
Skala : x = 2 : 8,72 kg/cm²

y = 1 : 1

POLIGON FREKUENSI

Poligon Frekuensi adalah suatu bentuk grafik yang digambarkan dengan menghubungkan titik-titik tengah dari garis puncak histogram dengan memakai garis lurus.

Contoh :

Poligon frekuensi hasil pemeriksaan keteguhan tekan beton (benda uji kubus sisi 15 cm) sesudah 28 hari engan campuran 1:2:3 yang dilaksanakan dilaboratorium pengujian bahan Politeknik UI Depok dalam satuan kg/cm².

keteguhan tekan beton (kg/cm2)

Keterangan :

Untuk melengkapi poligon frekuensi diawal dan diakhir distribusi frekuensi, masing-masing ditambah satu kelas dengan frekuensi = “ 0/nol “ sehingga poligon frekuensi komulatif dengan memakai garis lurus.

OGIVE FREKUENSI

Ogive frekuensi adalah suatu bentuk grafik yang merupakan bentuk penyajian distribusi frekuensi komulatif yang digambarkan dengna menghubungkan titik-titik dari frekuensi komulatif dengan memakai garis lurus.

Contoh :

a. Ogive Frekuensi “kurang dari (<)”hasil pemeriksaan keteguhan tekan beton (benda uji kubus sisi 15 cm) sesudah 28 hari engan campuran 1 : 2 : 3 yang dilaksanakan dilaboratorium pengujian bahan Politeknik UI Depok dalam satuan kg/cm²

keteguhan tekan beton (kg/cm2)

b. Ogive frekuensi “lebih dari (>)”hasil pemeriksaan keteguhan tekan beton (benda uji kubus sisi 15 cm) sesudah 28 hari engan campuran 1 : 2 : 3 yang dilaksanakan dilaboratorium pengujian bahan Politeknik UI Depok dalam satuan kg/cm²

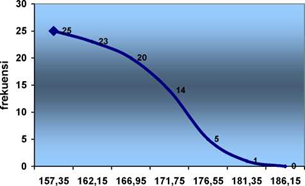
keteguhan tekan beton (kg/cm2)

Diagram lingkaran adalah suatu bentuk ddiagram yang berbentuk lingkaran dengan jari-jari yang membagi lingkaran itu menjadi beberapa daerah yang luasnya sesuai dengan frekuensinya, diman luas tersebut tergantung dari besar sudut.

(i° ) = Fi-j x 360°

keterangan : (i° ) = sudut pada kelas I

Contoh :

Diagram lingkaran hasil pemeriksaan keteguhan tekan beton (benda uji kubus sisi 15 cm) sesudah 28 hari engan campuran 1:2:3 yang dilaksanakan dilaboratorium pengujian bahan Politeknik UI Depok dalam satuan kg/cm²

Kelas (i)	Tanda Kelas (mi) (Kg/Cm2)	Frekuensi (fi)	Fri	Fri (%)	a (i)
1	159.75	2	0.08	8	28.8
2	164.55	3	0.12	12	43.2
3	169.35	6	0.24	24	86.4
4	174.15	9	0.36	36	129.6
5	178.95	4	0.16	16	57.6
6	183.75	1	0.04	4	14.4
	^7? = 25 Z=1	tFr, Z=1	/7’= I00″o	( i) = 360

Statistik Terapan Sem 3 D-IV Jalan Tol

RANGKUMAN

Distribusi Frekuensi Empiris adalah suatu daftar yang menunjukkan penggolongan kumpulan data diamana termasuk penentuan berapa bilangan yang termasuk ke dalam setiap golongan tersebut.

Variabel Penyelidikan adalah obyek yang diselidiki.

Distribusi Frekuensi Relatif adalah pencaran frekuensi yang diperoleh dengan membagi frekuensi tiap-tiap kelas dengan banyaknya data pengamatan

Distribusi Frekuensi komulaitf adalah pencaran frekuensi yang merupakan penjumlahan-penjumlahan frekuensi-frekuensi kelas secara berurutan.

Nilai variable adalah nilai masing-masing penyelidikan / pengujian. Distribusi Frekuensi Tunggal (DFT) adalah suatu pencaran frekuensi yang menunjukkan tidak adanya pengelompokkan nilai variabel.

Distribusi Frekuensi Bergolong (DFB) adalah suatu pencaran frekuensi yang menunjukkan adanya pengelompokkan nilai variabel dalam satu kelas.

Poligon Frekuensi adalah suatu bentuk grafik yang digambarkan dengan menghubungkan titik-titik tengah dari garis puncak histogram dengan memakai garis lurus.

Distribusi Frekuensi Relatif adalah pencaran frekuensi yang diperoleh dengan membagi frekuensi tiap-tiap kelas dengan banyaknya data pengamatan

Distribusi Frekuensi komulaitf adalah pencaran frekuensi yang merupakan penjumlahan-penjumlahan frekuensi-frekuensi kelas secara berurutan.

Histogram frekuensi adalah suatu bentuk diagram yang terdiri dari persegi panjang dimana setiap persegi panjang tersebut mewakili/ menerangkan/ menggambarkan sebuah kelas dari distribusi frekuensi. Poligon Frekuensi adalah suatu bentuk grafik yang digambarkan dengan menghubungkan titik-titik tengah dari garis puncak histogram dengan memakai garis lurus.

Ogive frekuensi adalah suatu bentuk grafik yang merupakan bentuk penyajian distribusi frekuensi komulatif yang digambarkan dengna menghubungkan titik-titik dari frekuensi komulatif dengan memakai garis lurus.

Diagram lingkaran adalah suatu bentuk ddiagram yang berbentuk lingkaran dengan jari-jari yang membagi lingkaran itu menjadi beberapa daerah yang luasnya sesuai dengan frekuensinya, diman luas tersebut tergantung dari besar sudut.

3.8 SOAL

1. Apa yang dimaksud dengan distribusi frekuensi empiris?
2. Apa yang dimaksud dengan distribusi frekuensi tunggal?
3. Apa yang dimaksud dengan distribusi frekuensi bergolong?
4. Apa yang dimaksud dengan distribusi frekuensi relatif?
5. Apa yang dimaksud dengan distribusi frekuensi komulatif?
6. Dibawah ini disajikan Data Volume Kendaraan Pada Ruas Jalan Tol Jakarta-Bogor-Ciawi untuk 50 Hari Kerja Pada Pukul 07.00 S/D 09.00 Pada Bulan Juli – September 2007 (Dalam Ratusan)

46.7	42.6	49.2	35.4	45.6
56.3	28.3	63.4	68.1	73.2
19.4	61.5	32.4	53.4	36.5
38.2	48.4	42.5	52.6	54.3
47.3	47.3	50.8	50.8	45.4
57.5	58.2	64.7	65.4	76.7
25.9	26.8	35.4	35.7	38.1
37.3	50.3	52.1	60.1	57.1
42.3	46.8	48.6	56.8	68.0
40.8	40.1	44.6	44.2	46.9

1. Buatlah distribusi frekuensi bergolong, relatif dan komulatif.

• Gambarkan histogram, polygon, diagram lingkaran, ogive frekuensi dari distribusi frekuensi diatas.