Time Value Of Money

Time Value of Money (TVM) “dalam bahasa nilai uang atas waktu” adalah konsep keuangan yang mengartikan bahwa nilai suatu uang lebih berharga/bernilai pada saat ini daripada besar uang yang sama di waktu mendatang karena potensi pendapatan uang tersebut. atau bisa juga dikatakan bahwa1 Rupiah sekarang nilainya lebih berharga daripada 1 Rupiah di masa yang akan datang. 

1. KONSEP DASAR

Menggunakan timelines untuk memvisualisasikan arus kas 

• Suatu timeline menggambarkan waktu dan jumlah skema pembayaran – baik kas yang diterima dan cash yang dikeluarkan – bersamaan dengan tingkat bunga yang ditetapkan. 
• Suatu timeline biasanya digambarkan dalam tahunan, tetapi bisa juga digambarkan secara bulanan, harian, atau satuan waktu lainnya.
• Timeline

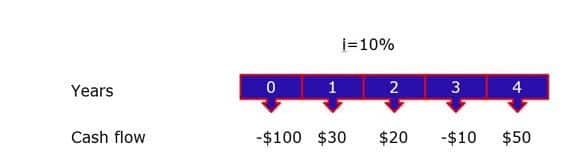
Timeline diatas menunjukkan arus kas keluar sebesar $100 terjadi di tahun pertama, kemudian arus kas masuk sebesar $30 dan $20 di tahun kedua dan ketiga, cash outflow $10, cash inflow $50 

Perhitungan time value of money adalah Present Value (Nilai yang wajar di masa sekarang) dan Future Value (nilai yang wajar di masa yang akan datang

2. Compounding and Future Value

Penghitungan time value of money meliputi Present value (berapa nilai arus kas saat ini) dan  Future value (berapa nilai arus kas di masa yang akan datang).

Contoh :

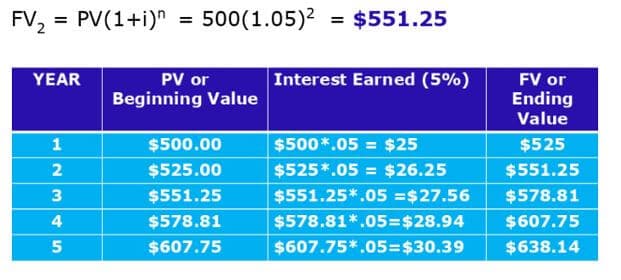
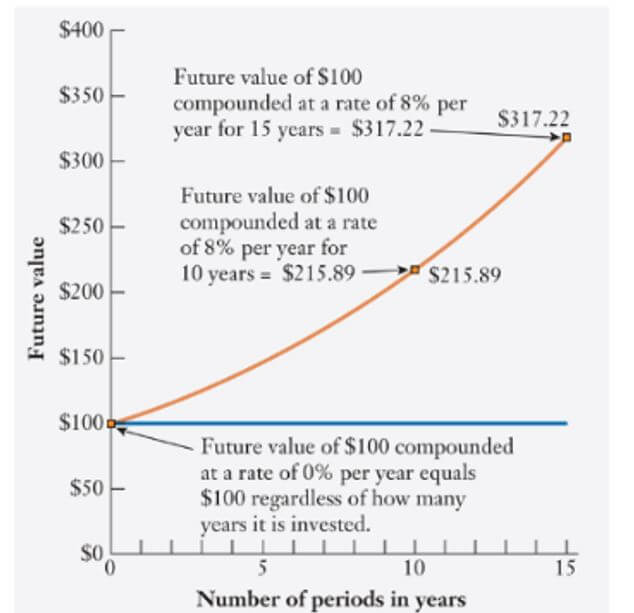
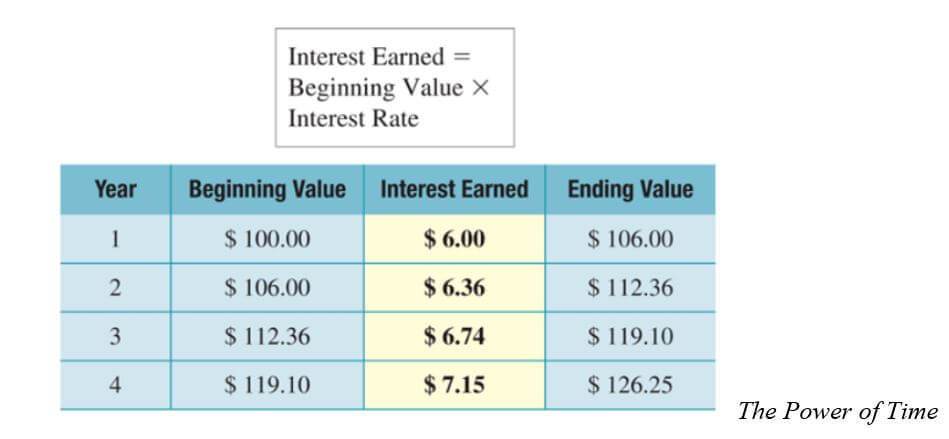
Suppose that you deposited $500 in your savings account that earns 5% annual interest. How much will you have in your account after two years? After five years?

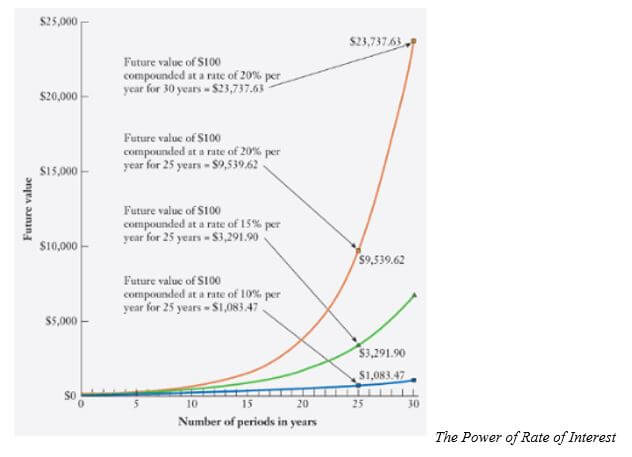
Compound Interest with Shorter Compounding Periods

Bank biasanya menawarkan akun tabungan yang memajemukan bunga secara harian, bulanan, atau pertiga bulanan. Semakin sering dimajemukan akan menghasilkan pendapatan bunga yang semakin tinggi dan menjadikan nilai FV-nya juga semakin tinggi.

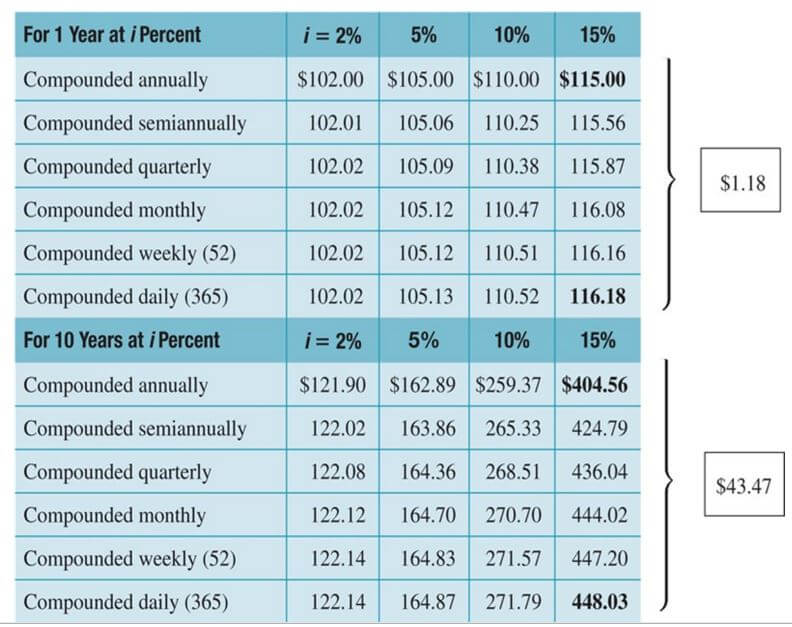
Contoh :

If you deposit $50,000 in an account that pays an annual interest rate of 10% compounded monthly, what will your account balance be in 10 years?

Jawab :

3. Discounting and Present Value

Pertanyaan Kunci : 

• Berapakah nilai saat ini atas arus kas yang akan diterima di masa yang akan datang? 
• Jawaban atas pertanyaan ini memerlukan penghitungan present value (PV) yaitu nilai hari ini atas arus kas masa depan, dan proses discounting. 

Contoh :

What is the present value of $100,000 to be received at the end of 25 years given a 5% discount rate?

Jawab  :

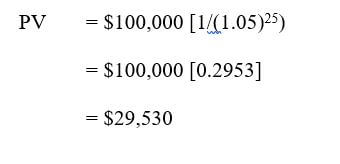
4. The Rule of 72

Aturan 72 dapat digunakan untuk menentukan berapa tahun supaya investasi kita menjadi 2x lipat. 

N = 72/interest rate 

Contoh : 

Apabila kita menginvestasikan dengan tingkat bunga 8%, maka kita memebutuhkan waktu 9 tahun  (N = 72/8) agar investasi kita menjadi 2x lipat

5. Problem untuk menentukan jumlah periode

Berapa tahun yang diperlukan agar uang seharga  $10.000 menjadi $200.000 apabila tingkat bunga 15% tahunan?

6. Problem untuk menentukan tingkat bunga :

Pada tingkat bunga berapa uang sebesar $50.000 akan menjadi $1.000.000 dalam jangka waktu 30 tahun?

Annual Percentage Rate (APR) 

APR menunjukkan tingkat bunga yang diterima selama 1 tahun tanpa kemajemukan (bulanan, harian, triwulanan). APR juga biasa disebut nominal or quoted interest. 

Kita tidak bias membandingkan 2 hutang dengan APR jika memiliki periode pembayaran berbeda (harian, bulanan, tahunan, atau yang lain). Untuk bisa dibandingkan, kita cari EAR nya yaitu tingkat bunga yang didapat selama 1 tahun.

Contoh : 

Berapa EAR jika nominal rate nya 13% yang buganya dibayarkan bulanan?

EAR nya 13,8% menunjukkan jika bunga dibayarkan secara tahunan, maka tingkat bunganya 13,8% (sama dengan tingkat bunga 13% dibayar bulanan).